... (SVG)¹

Vgl. Scalable Vector Graphics (SVG) http://www.w3.org/Graphics/SVG/http://www.w3.org/Graphics/SVG/

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... W3C²

Vgl. World Wide Web Consortium (W3C) http://www.w3.orghttp://www.w3.org.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... XML³

Vgl. Extensible Markup Language (XML) http://www.w3.org/XML/http://www.w3.org/XML/

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... B\'ezierkurven⁴

Die Erklärung einer quadratischen bzw. kubischen Bézierkurve erfolgt in Kapitel 2.3.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... wird⁵

Vgl. Wikipedia [4]: ,,Polygon``

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... eingezeichnet⁶

mod soll als Operator fungieren. Es soll bei der ganzzahligen Division mit Rest den Rest zurückgeben.

Beispiel: $42\bmod 10 = 2$

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

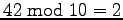
... Linienverlauf⁷

Vgl. Wikipedia [4]: ,,Polygonzug``

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... Polygonzug⁸

Vgl. Abbildung 12.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...⁹

Die Gleichungen werden ohne explizite Angabe der entsprechenden Vektoren angegeben, obwohl diese in den vorherigen Kapiteln festgelegt wurden. Dies hat den Vorteil, dass die Gleichungen leichter, durch Austauschen der entsprechenden Formel für die Vektoren, entsprechend der jeweiligen Polygone angepasst werden können.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... Gleichungen¹⁰

Die Formeln werden hier nicht im Text eingefügt, da diese den Lesefluss erheblich stören würden. Die Formeln sind dem jeweilig angegeben Unterkapitel zu entnehmen. Auf die ersten drei Gleichungen (siehe Kapitel A.1.1 bis A.1.3) wird zudem in späteren Überlegungen kein Bezug genommen, deswegen werden sie in dieser Arbeit nicht genauer erläutert.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... gesetzt¹¹

Die Auswirkungen der Wahl des Wertes der Parameter wird in Kapitel 5.1 erläutert

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... Eliminationsverfahren¹²

Vgl. Trapp [1], Seite 67ff., Satz 9.2

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... System¹³

Vgl. Trapp [1], Seite 68, Satz 9.4

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... genannt¹⁴

Vgl. Felgenhauer [3], Seite 23, Definition 2.2

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... b-Spalte¹⁵

Als b-Spalte soll die letzte Spalte im Gleichungssystem benannt werden.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... Schritten¹⁶

Für die Variablen gelte im Folgenden: 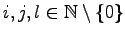$i,j,l \in \mathbb{N} \setminus \left\lbrace 0 \right\rbrace$ und $l\neq j$

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

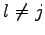
... Formeln¹⁷

Vgl. Gleichungen 2 bis 5.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... Unterraum¹⁸

Vgl. Trapp [1], Seite 78, Satz 11.6

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... eingeschränkt¹⁹

Vgl. Felgenhauer [3], Seite 21

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... eingenommen²⁰

Vgl. Felgenhauer [3], Seite 21, Satz 2.2

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... wird²¹

Vgl. Felgenhauer [3], Seite 27

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... wird²²

Vgl. Felgenhauer [3], Seite 27

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... erreicht²³

Vgl. Felgenhauer [3], Seite 29f.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... übertragen²⁴

Weitere Erläuterungen können dem später folgendem Kapitel 5.2 entnommen werden.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... Polygons²⁵

Vgl. Gleichung 9

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... darf²⁶

Vgl. Kapitel 3.2.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... beschreibt²⁷

Vgl. Kapitel 4

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... Java²⁸

Version 1.5.0, siehe auch http://java.sun.com/j2se/1.5.0/http://java.sun.com/j2se/1.5.0/

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... werden²⁹

Weiterführende Informationen können der Java Dokumentation, die auf der beigefügten CD-ROM vorliegt.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... nicht³⁰

siehe Gleichung 11

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... Kapiteln³¹

Vgl. Kapitel 3.1.3

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... B\'ezierkurve³²

Die Spezifikationen in der die Bézierkurve in der SVG Datei gespeichert wurde sind dem Buch von Eisenberg [2] entnommen.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... Punkt³³

Aus dem Paket poly2bezier.material

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... Vector³⁴

Aus dem Paket java.util

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... poly2Kurve()³⁵

In der Klasse poly2bezier.Punkte2KubBezier

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... Vector³⁶

Aus dem Paket java.util

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... Objekt³⁷

Es muss eigentlich die ,,Referenz auf dieses Vector Objekt`` heißen. Auf diese Feinheiten wurde u. a. auf Grund der Lesbarkeit des Textes verzichtet.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... canDelete()³⁸

In der Klasse poly2bezier.material.PolyMaterial

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... split2Segments()³⁹

In der Klasse poly2bezier.material.PolyMaterial

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... getRichtung()⁴⁰

In der Klasse poly2bezier.material.PolyMaterial

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... segment2Kurve()⁴¹

In der Klasse poly2bezier.Punkte2KubBezier

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... BezierFormeln⁴²

Aus dem Paket poly2bezier.material

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... BezierFormeln⁴³

Aus dem Paket poly2bezier.material

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... Converter⁴⁴

Aus dem Paket poly2bezier.material

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... findMinAlgo()⁴⁵

In der Klasse poly2bezier.material.Gleichungssystem

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... segment2Kurve()⁴⁶

In der Klasse poly2bezier.Punkte2KubBezier

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... BezierFormeln⁴⁷

Aus dem Paket poly2bezier.material

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... unionSegments()⁴⁸

In der Klasse poly2bezier.Punkte2KubBezier

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... nutzen⁴⁹

Die graphische Oberfläche ist ebenfalls im Internet als Applet, mit eingeschränkten Funktionen, aufrufbar. http://www-lehre.inf.uos.de/ kkleinek/Bachelor/Applet.htmlhttp://www-lehre.inf.uos.de/ kkleinek/Bachelor/Applet.html

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... Projektes⁵⁰

vgl. http://xml.apache.org/batikhttp://xml.apache.org/batik

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... Kommandozeile⁵¹

Der Implementation sind vier Beispieldateien beigefügt. Sie tragen die Endung .dat.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.