Nächste Seite: Die Auswirkungen der Parameter Aufwärts: Approximation von Bézierkurven durch Vorherige Seite: Nicht konvexe Polygone und Inhalt
In den vorangegangenen Kapiteln erfolgte die Approximation von Polygonzügen nur durch quadratische Bézierkurven. In diesem Kapitel soll die Approximation von Polygonen und Polygonzügen durch kubische Bézierkurven betrachtet werden. Diese wird auf die Approximation durch quadratische Bézierkurven zurückgeführt.
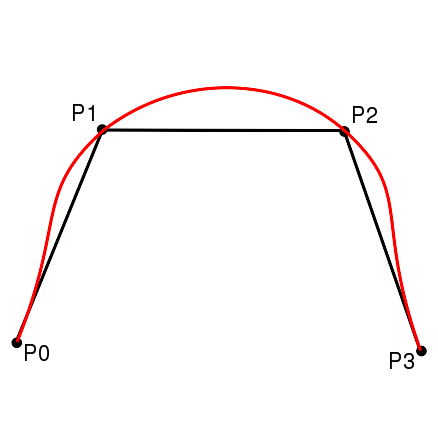
In Abbildung 24 ist eine Polygonkante mit den Kontrollpunkten und den Strecken zwischen den Kontrollpunkten einer quadratischen Bézierkurve gezeigt. Da für die kubischen Bézierkurven ebenfalls die gleichen Bedingungen für die Tangenten in den Endpunkten ![]() und
und ![]() gelten sollen, wie für die quadratischen Bézierkurven, müssen sich die zwei Kontrollpunkte
gelten sollen, wie für die quadratischen Bézierkurven, müssen sich die zwei Kontrollpunkte ![]() und
und ![]() der kubischen Bézierkurve auf der Strecke zwischen den Kontrollpunkten einer entsprechenden quadratischen Bézierkurve befinden, welche die selbe Kante approximieren würde. Die Verschiebung der Punkte auf dieser Strecke ist ein Freiheitsgrad, der in den Gleichungen für jeden mittleren Kontrollpunkt hinzukommt.
der kubischen Bézierkurve auf der Strecke zwischen den Kontrollpunkten einer entsprechenden quadratischen Bézierkurve befinden, welche die selbe Kante approximieren würde. Die Verschiebung der Punkte auf dieser Strecke ist ein Freiheitsgrad, der in den Gleichungen für jeden mittleren Kontrollpunkt hinzukommt.
Wenn sich die beiden mittleren Kontrollpunkte nahe der Kontrollpunkte am Ende der elementaren Bézierkurve befinden (siehe Abbildung 25), ergibt sich eine sehr flache Bézierkurve, die sich sehr nahe an der Polygonkante befindet und somit den Polygonzug besser approximiert. Dieser Freiheitsgrad stellt ein gravierendes Problem dar, wenn er in die Gleichungen aufgenommen wird. Da der Algorithmus auf Minimierung der Abstände ausgerichtet wurde, wird er die mittleren Kontrollpunkte mit den Kontrollpunkten an den Enden gleichsetzen, wenn ihm die Wahl überlassen wird, und somit die Abstände auf den Wert Null bringen, aber dadurch keine stetige Bézierkurve erzeugen. Ein weiteres Problem ist, dass je weiter sich die mittleren Kontrollpunkte den Endpunkten näheren, desto enger wird die Kurve von einer elementaren Bézierkurve zur nächsten.
Um diesen Freiheitsgrad am besten nutzen zu können, wurde die Entscheidung auf den Benutzer übertragen24.
Dazu wird ein Parameter ![]() eingeführt, der festlegt, an welcher Stelle die Kontrollpunkte für die kubische Bézierkurve liegen sollen. Der Parameter beschreibt des Verhältnis, in das die Strecke zwischen Endpunkt und Kontrollpunkt einer quadratischen Bézierkurve durch den Kontrollpunkt einer entsprechenden kubischen Bézierkurve geteilt wird. Je kleiner das Verhältnis ist, desto näher liegen die Kontrollpunkte der kubischen Bézierkurve an den Endpunkten, desto besser ist die Approximation und desto enger ist die Kurve an den Übergängen.
eingeführt, der festlegt, an welcher Stelle die Kontrollpunkte für die kubische Bézierkurve liegen sollen. Der Parameter beschreibt des Verhältnis, in das die Strecke zwischen Endpunkt und Kontrollpunkt einer quadratischen Bézierkurve durch den Kontrollpunkt einer entsprechenden kubischen Bézierkurve geteilt wird. Je kleiner das Verhältnis ist, desto näher liegen die Kontrollpunkte der kubischen Bézierkurve an den Endpunkten, desto besser ist die Approximation und desto enger ist die Kurve an den Übergängen.
Für die kubischen Bézierkurven muss eine Änderung in den Gleichungen vorgenommen werden. Die Gleichungen für die quadratische Bézierkurve werden durch folgende Gleichungen der kubischen Bézierkurve ausgetauscht.
| (12) | |||
| (13) | |||
| (14) | |||
| (15) | |||
| (16) | |||
| (17) |
Alternativ wäre eine Neuaufstellung von Bedingungen für die Endkanten denkbar, so dass die Parameter ![]() und
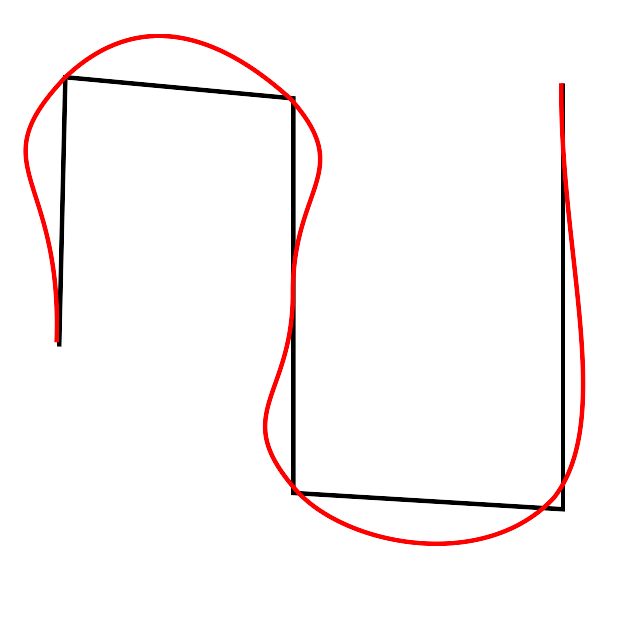
und ![]() nicht auf den Null gesetzt werden müssen. Dies folgt daraus, dass die kubischen Bézierkurven, im Gegensatz zu den quadratischen, für Richtungswechsel genutzt werden können. Somit ist es möglich, Bedingungen aufzustellen, die einer Bézierkurve entsprechen würden, welche die Endkanten approximiert, wie es in Abbildung 26 zu sehen ist. Wenn nun aber die nicht konvexen Polygone unter Verwendung dieser Bedingungen approximiert werden, führt dies zu dem Auftreten von oszillierendem Verhalten an den Übergängen (siehe Abbildung 27). Dies ergibt aber keine gute Approximation.
nicht auf den Null gesetzt werden müssen. Dies folgt daraus, dass die kubischen Bézierkurven, im Gegensatz zu den quadratischen, für Richtungswechsel genutzt werden können. Somit ist es möglich, Bedingungen aufzustellen, die einer Bézierkurve entsprechen würden, welche die Endkanten approximiert, wie es in Abbildung 26 zu sehen ist. Wenn nun aber die nicht konvexen Polygone unter Verwendung dieser Bedingungen approximiert werden, führt dies zu dem Auftreten von oszillierendem Verhalten an den Übergängen (siehe Abbildung 27). Dies ergibt aber keine gute Approximation.
|
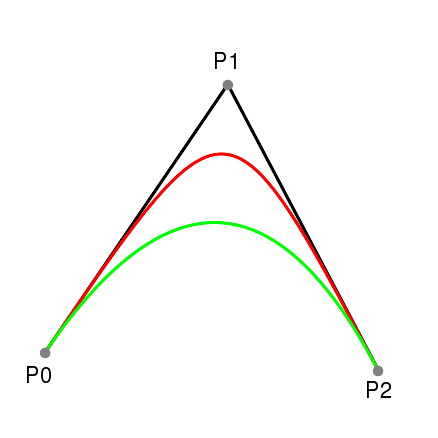
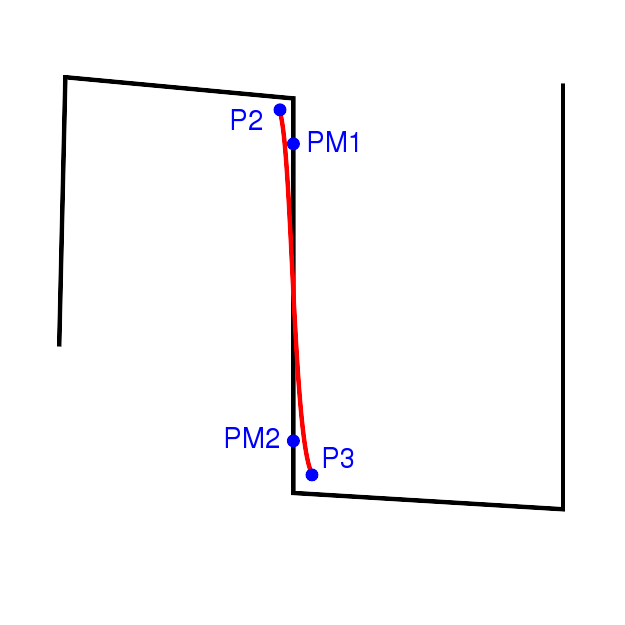
Die Polygonzüge, die aus drei Punkten bestehen, werden durch eine kubische Bézierkurve approximiert, indem die mittleren Kontrollpunkte beide mit dem mittleren Punkt gleichgesetzt werden. Die kubische Bézierkurve ist dadurch näher an den Polygonkanten, als die quadratische Bézierkurve mit den gleichen Vorteilen und es müssen keine zusätzlichen Berechnungen durchgeführt werden (siehe Abbildung 28).
|
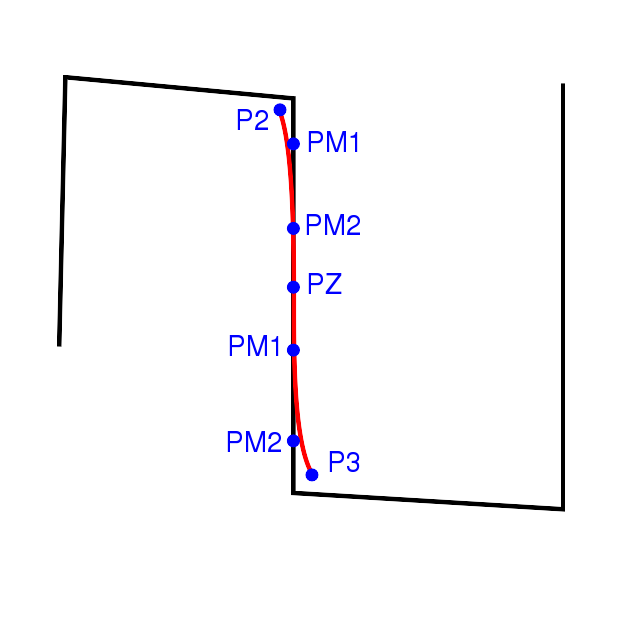
Die nicht konvexen Polygone und Polygonzüge werden bei der Approximation auf die konvexen Polygonzüge zurückgeführt. Beim Zusammensetzen der einzelnen konvexen Segmente gibt es im Gegensatz zu der Approximation durch quadratische Bézierkurven eine Alternative. Da die kubischen Bézierkurven zur Darstellung eines Richtungswechsels herangezogen werden können, muss eine Kante, die einen solchen Übergang enthält, nicht durch zwei kubische Bézierkurven approximiert werden. In Abbildung 29 ist eine solche Kante mit den entsprechenden Kontrollpunkten gegeben. Die zwei elementaren Bézierkurven können zu einer elementaren Bézierkurve zusammengefasst werden, indem die mittleren drei Kontrollpunkte entfernt werden. In Abbildung 30 ist das Ergebnis gezeigt. Dies führt zu einer Verminderung der Komplexität und des Aufwands der Darstellung. Der Grad der Approximation wird dabei aber nicht wesentlich verschlechtert. Trotz dieser Vorteile wird dieses Verfahren in dieser Arbeit aber nicht verwendet, da es in Kombination mit der Vorgehensweise bei der Approximation von Polygonzügen die nur drei Kontrollpunkte besitzen, nicht verwendet werden kann.
|
Nachdem die Approximation von Polygonen und Polygonzügen nun sowohl durch quadratische als auch durch kubische Bézierkurven gezeigt wurde, soll ein Vergleich dieser beiden Möglichkeiten durchgeführt werden. Die Verwendung von kubischen Bézierkurven führt zu einem harmonischerem Aussehen der berechneten Bézierkurven. Damit geht allerdings ein erheblich größerer Aufwand bei der Darstellung einher. Dies mag bei einzelnen Polygonen keine deutlich negativen Auswirkungen haben, doch wenn die Anzahl an Polygonen größer ist, kann die Rechenkapazität schnell an ihre Grenzen stoßen. Zur Verdeutlichung soll hier ein praktisches Beispiel gegeben werden. Eine Fläche der Größe der Bundesrepublik Deutschland, soll auf dem Bildschirm dargestellt werden. Angenommen ein Raster an Messpunkten, das auf diesen Gebiet liegt, aus deren Werten Isolinien berechnet wurden, hat eine Dichte von 10 mal 10 Kilometern. Sollten die Polygone, welche dann die Isolinien wiedergeben, alle dargestellt werden, summiert sich der Rechenaufwand pro elementarer Bézierkurve, also pro Kante der Polygone, schnell zu einem immensen Wert. Bei der Approximation durch quadratische Bézierkurven ist der Aufwand pro Kante geringer. Allerdings sind sie nicht in der Lage die Polygone und Polygonzüge so gut zu approximieren. Die Wahl zwischen den beiden Möglichkeiten der Approximation sollte also genau abgewogen und auf die jeweilige Situation abgestimmt sein. Die Approximation vieler Polygone durch kubische Bézierkurven ist nur dann möglich, wenn die Rechenkapazität, die zur Darstellung nötig ist, bereitgestellt werden kann. Darüber hinaus sollten auch die nötige Genauigkeit der Darstellung berücksichtigt werden. Wenn keine besondere Genauigkeit notwendig ist, bietet sich die Verwendung von quadratischen Bézierkurven an.
Karl kleine Kruse 2007-09-16