Nächste Seite: Zusammenfassung Aufwärts: Konvexe Polygone Vorherige Seite: Aufstellen eines Gleichungssystems Inhalt
Die Lösung eines linearen Gleichungssystem ist nach der linearen Algebra ein linearer Unterraum (im Weiteren LU genannt). Jeder Punkt in diesem LU beschreibt eine Bézierkurve, aber nicht jeder Punkt in diesem LU beschreibt nach den bis jetzt genannten Kriterien eine gültige Bézierkurve. Im LU können die Parameter negative Werte annehmen, die hier ungültig sind. Der optimale Punkt im LU, der die Parameter für die Bézierkurve beschreibt, hat die Eigenschaft, dass alle Einträge positiv sind. Des Weiteren sollte die Abweichung der Bézierkurve vom Polygon minimal sein und somit auch die Summe aller Einträge des Punktes. Dieser Punkt kann durch Umformung des Gleichungssystems ermittelt werden.
Dazu muss vorab geklärt werden, ob es überhaupt für jedes Polygon eine Bézierkurve gibt, die alle Kriterien erfüllt. Andernfalls würde ein Punkt gesucht werden, der nicht im LU vorhanden ist. Im Falle eines konvexen Polygons existiert allerdings immer ein solcher Punkt, der eine gültige Bézierkurve beschreibt. Die Bézierkurve dessen Graph durch die Eckpunkte des Polygons verläuft, erfüllt alle Kriterien. Die Werte der Parameter ![]() sind Null, sowie die der Parameter
sind Null, sowie die der Parameter ![]() größer Null, da die Tangenten in den Eckpunkten die Kontrollpunkte vorgeben. In Abbildung 17 ist ein Beispiel gezeigt. Unabhängig davon wie ein konvexes geschlossenes Polygon verläuft, die Bézierkurve durch die Eckpunkte ist eine gültige Lösung nach diesen Kriterien. Da also immer eine Lösung vorhanden ist, muss durch Wahl eines geeigneten Suchverfahrens der optimale Punkt im LU ermittelt werden.
größer Null, da die Tangenten in den Eckpunkten die Kontrollpunkte vorgeben. In Abbildung 17 ist ein Beispiel gezeigt. Unabhängig davon wie ein konvexes geschlossenes Polygon verläuft, die Bézierkurve durch die Eckpunkte ist eine gültige Lösung nach diesen Kriterien. Da also immer eine Lösung vorhanden ist, muss durch Wahl eines geeigneten Suchverfahrens der optimale Punkt im LU ermittelt werden.
Ein Gleichungssystem kann nach dem Gauß'schen Eliminationsverfahren12 vereinfacht werden, so dass eine Hauptdiagonale entsteht. Dazu wird wie folgt vorgegangen: Es werden die Gleichungen von oben im Gleichungssystem angefangen, also von der 1-sten Zeile, der Reihe nach umgeformt, also bis zur ![]() -ten Zeile. Dabei weist das zum Gleichungssystem gehörige Polygon
-ten Zeile. Dabei weist das zum Gleichungssystem gehörige Polygon ![]() Kanten auf. Zuerst wird die entsprechende Zeile, angenommen die j-te, normiert, so dass der j-te Eintrag in der j-ten Zeile auf Eins normiert wird. Das wird erreicht indem die j-te Zeile durch den Eintrag
Kanten auf. Zuerst wird die entsprechende Zeile, angenommen die j-te, normiert, so dass der j-te Eintrag in der j-ten Zeile auf Eins normiert wird. Das wird erreicht indem die j-te Zeile durch den Eintrag ![]() dividiert wird, sofern
dividiert wird, sofern
![]() . Anschließend werden die Zeilen unterhalb der j-ten Zeile umgeformt, so dass in der j-ten Spalte unterhalb des j-ten Eintrags nur noch Nullen vorhanden sind, indem von den unteren Zeilen die j-te Zeile mit einem passendem Faktor abgezogen wird. Diese Schritte sind an folgendem Gleichungssystem gezeigt. Das Gleichungssystem enthält nur 3 Gleichungen, da es nur die Schritte der Umformung veranschaulichen soll.
. Anschließend werden die Zeilen unterhalb der j-ten Zeile umgeformt, so dass in der j-ten Spalte unterhalb des j-ten Eintrags nur noch Nullen vorhanden sind, indem von den unteren Zeilen die j-te Zeile mit einem passendem Faktor abgezogen wird. Diese Schritte sind an folgendem Gleichungssystem gezeigt. Das Gleichungssystem enthält nur 3 Gleichungen, da es nur die Schritte der Umformung veranschaulichen soll.
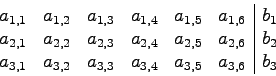
1. Schritt: Normieren der 1. Zeile
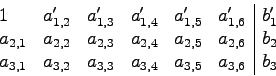
2. Schritt: Erzeugen der Nullen
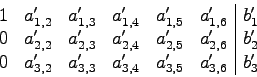
Restlichen Zeilen analog
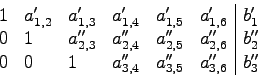
Um die restlichen Einträge zu dem Wert Null umzuformen, wird analog vorgegangen. Diesmal wird von der ![]() -ten Zeile beginnend nach oben und von der
-ten Zeile beginnend nach oben und von der ![]() -ten Spalte nach links umgeformt. Das Normieren entfällt und die Einträge in der j-ten Spalte über dem j-ten Eintrag werden zum Wert Null umgeformt, indem die j-te Zeile mit dem entsprechenden Faktor von der jeweiligen Zeile abgezogen wird. Dies wird wiederum am Gleichungssystem, das zu einem Reduzierten System13 umgeformt wird, verdeutlicht.
-ten Spalte nach links umgeformt. Das Normieren entfällt und die Einträge in der j-ten Spalte über dem j-ten Eintrag werden zum Wert Null umgeformt, indem die j-te Zeile mit dem entsprechenden Faktor von der jeweiligen Zeile abgezogen wird. Dies wird wiederum am Gleichungssystem, das zu einem Reduzierten System13 umgeformt wird, verdeutlicht.
Die oberen Nullen erzeugen
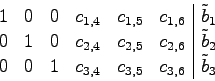
Beim Erzeugen der Hauptdiagonalen ist Folgendes zu berücksichtigen. An der Stelle ![]() muss zum Einen nicht immer ein Eintrag sein, dessen Wert ungleich Null ist. Somit könnte dann keine Normierung durchgeführt werden. Das Gleichungssystem wird aber so aufgestellt, dass die Einträge auf der Hauptdiagonalen immer ungleich Null sind. Das Gleichungssystem für ein konvexes Polygon mit
muss zum Einen nicht immer ein Eintrag sein, dessen Wert ungleich Null ist. Somit könnte dann keine Normierung durchgeführt werden. Das Gleichungssystem wird aber so aufgestellt, dass die Einträge auf der Hauptdiagonalen immer ungleich Null sind. Das Gleichungssystem für ein konvexes Polygon mit ![]() Kanten soll folgende Form haben.
Kanten soll folgende Form haben.
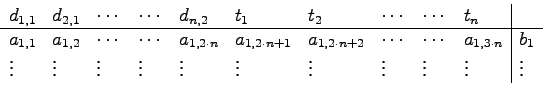
Das Gleichungssystem wird so aufgebaut, dass die Gleichungen entsprechend der Reihenfolge der Parameter in das Gleichungssystem eingetragen werden. Folglich steht in der ersten Zeile die Gleichung mit ![]() , dann die mit
, dann die mit ![]() usw., so dass die Gleichung für
usw., so dass die Gleichung für ![]() in der
in der ![]() ten Zeile steht. Aus diesem Aufbau ergibt sich eine Hauptdiagonale, die nur noch normiert werden muss. Dies folgt aus der Tatsache, dass in jeweils einer Gleichung nur ein Parameter
ten Zeile steht. Aus diesem Aufbau ergibt sich eine Hauptdiagonale, die nur noch normiert werden muss. Dies folgt aus der Tatsache, dass in jeweils einer Gleichung nur ein Parameter ![]() und die Parameter
und die Parameter ![]() und
und ![]() auftreten (siehe Gleichung 11).
auftreten (siehe Gleichung 11).
Das obige System kann nur Verwendung finden, wenn die Anzahl der freien Variablen höher ist als die der Gleichungen. Da dies bei konvexen Polygonen der Fall ist, kann diese Vorgehensweise bei diesen zur Anwendung kommen. Bei einem Polygon mit ![]() Punkten, gibt es
Punkten, gibt es ![]() Kanten die zu approximieren sind. Das bedeutet, das für jede Kante zwei Gleichungen aufgestellt werden müssen und das Gleichungssystem
Kanten die zu approximieren sind. Das bedeutet, das für jede Kante zwei Gleichungen aufgestellt werden müssen und das Gleichungssystem ![]() Gleichungen enthält. Für jeden Eckpunkt existiert ein freier Parameter
Gleichungen enthält. Für jeden Eckpunkt existiert ein freier Parameter ![]() und für jede Kante zwei Parameter
und für jede Kante zwei Parameter ![]() . Daraus folgt, dass es
. Daraus folgt, dass es ![]() freie Variablen gibt, also
freie Variablen gibt, also ![]() mehr als Gleichungen.
mehr als Gleichungen.
Ein Punkt des LU kann berechnet werden, indem alle Parameter bis auf die ersten ![]() des Gleichungssystems mit
des Gleichungssystems mit ![]() Gleichungen auf Null gesetzt und die restlichen dann berechnet werden. Die so berechnete Lösung wird Basislösung des Gleichungsystems genannt14.
Der Lösungsvektor entspricht der b-Spalte15
die um Null-Einträge ergänzt worden ist. Da nach dem vorher genannten Aufbau alle Werte der
Gleichungen auf Null gesetzt und die restlichen dann berechnet werden. Die so berechnete Lösung wird Basislösung des Gleichungsystems genannt14.
Der Lösungsvektor entspricht der b-Spalte15
die um Null-Einträge ergänzt worden ist. Da nach dem vorher genannten Aufbau alle Werte der ![]() zu Beginn auf Null gesetzt wurden, entspricht die Anfangslösung einer gültigen Lösung. Die Basislösung muss aber nicht die bestmögliche Bézierkurve wiedergeben. Dazu werden nun Überlegungen durchgeführt, wie von dieser Basislösung zu einer besseren Basislösung übergegangen werden kann.
zu Beginn auf Null gesetzt wurden, entspricht die Anfangslösung einer gültigen Lösung. Die Basislösung muss aber nicht die bestmögliche Bézierkurve wiedergeben. Dazu werden nun Überlegungen durchgeführt, wie von dieser Basislösung zu einer besseren Basislösung übergegangen werden kann.
Ein Gleichungssystem, mit dessen Hilfe ein Lösungsvektor berechnet wurde, hat nach Bildung einer Hauptdiagonalen folgende Gestalt.
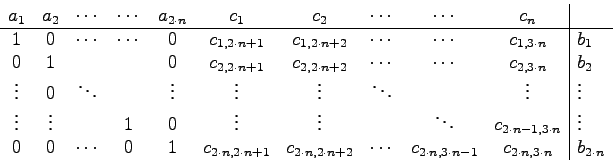
Da der Lösungsvektor berechnet wird, indem die Werte der Variablen ![]() bis
bis ![]() auf Null gesetzt werden, ist die Summe der Einträge der Basislösung gleich der Summe der Einträge der b-Spalte. Im Folgenden soll mit Min-Schritt eine Umformung im Gleichungssystem bezeichnet werden, die eine Verringerung der Summe der Einträge der b-Spalte zur Folge hat, aber nicht zu einer ungültigen Lösung führt. Dieses Verfahren basiert auf dem Simplex-Algorithmus. Der angewendete Min-Schritt ist dem Austauschschritt des Simplex-Algorithmus ähnlich. In diesem Verfahren, wird aber auf die Zielfunktion verzichtet, da immer die Summe aller Einträge berechnet werden soll.
auf Null gesetzt werden, ist die Summe der Einträge der Basislösung gleich der Summe der Einträge der b-Spalte. Im Folgenden soll mit Min-Schritt eine Umformung im Gleichungssystem bezeichnet werden, die eine Verringerung der Summe der Einträge der b-Spalte zur Folge hat, aber nicht zu einer ungültigen Lösung führt. Dieses Verfahren basiert auf dem Simplex-Algorithmus. Der angewendete Min-Schritt ist dem Austauschschritt des Simplex-Algorithmus ähnlich. In diesem Verfahren, wird aber auf die Zielfunktion verzichtet, da immer die Summe aller Einträge berechnet werden soll.
Ein Min-Schritt besteht aus den folgenden, beispielhaft an einem kleinen Gleichungssystem gezeigten, Schritten16:
Eintrag ![]() wird gewählt.
wird gewählt.
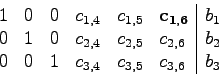
Tauschen der Spalten 6 und 3.
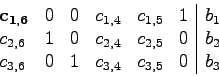
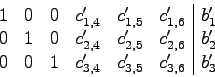
Zu klären ist nun, welchen Kriterien der Eintrag ![]() , der zu einer Verringerung der Summe führen soll, entsprechen muss. Je nach Wahl des Eintrags
, der zu einer Verringerung der Summe führen soll, entsprechen muss. Je nach Wahl des Eintrags ![]() , ergibt sich nach Durchführung des Min-Schrittes, eine entsprechende b-Spalte und somit auch eine entsprechende Basislösung. Um die Kriterien, die an den Eintrag
, ergibt sich nach Durchführung des Min-Schrittes, eine entsprechende b-Spalte und somit auch eine entsprechende Basislösung. Um die Kriterien, die an den Eintrag ![]() gestellt werden, zu bestimmen, wird der dritte Schritt genauer untersucht, da der erste und der zweite Schritt keine Veränderung der b-Spalte erzeugen und somit auch keine Veränderung der Basislösung.
gestellt werden, zu bestimmen, wird der dritte Schritt genauer untersucht, da der erste und der zweite Schritt keine Veränderung der b-Spalte erzeugen und somit auch keine Veränderung der Basislösung.
Der dritte Schritt kann wiederum in zwei Teile unterteilt werden. Im ersten Teil wird die Zeile durch den Eintrag ![]() dividiert. Wenn der Eintrag
dividiert. Wenn der Eintrag ![]() negativ war, ergibt sich eine nicht gültige Basislösung, da mit einer gültigen Anfangslösung begonnen wurde. Der Eintrag
negativ war, ergibt sich eine nicht gültige Basislösung, da mit einer gültigen Anfangslösung begonnen wurde. Der Eintrag ![]() war daher vorher positiv und wird durch das Dividieren mit einem negativen Eintrag
war daher vorher positiv und wird durch das Dividieren mit einem negativen Eintrag ![]() negativ. Die erste Einschränkung für
negativ. Die erste Einschränkung für ![]() besteht somit darin, dass dieser Eintrag positiv sein muss, um bei einer korrekten Basislösung zu bleiben. Darüber hinaus darf der Eintrag
besteht somit darin, dass dieser Eintrag positiv sein muss, um bei einer korrekten Basislösung zu bleiben. Darüber hinaus darf der Eintrag ![]() nicht den Wert Null haben, um den Austausch der Spalten durchführen zu können. Wenn der Eintrag Null wäre, könnte durch den beschriebenen Min-Schritt keine Hauptdiagonale entstehen.
nicht den Wert Null haben, um den Austausch der Spalten durchführen zu können. Wenn der Eintrag Null wäre, könnte durch den beschriebenen Min-Schritt keine Hauptdiagonale entstehen.
Im zweiten Teil wird dann von den übrigen Zeilen das ![]() -te der
-te der ![]() -ten Zeile von der
-ten Zeile von der ![]() -ten Zeile abgezogen, wobei gilt
-ten Zeile abgezogen, wobei gilt ![]() . Da dies zu Veränderungen in der b-Spalte führt, ist darauf zu achten, dass die Einträge in der b-Spalte nicht negativ werden oder dass es zu einer Vergrößerung der Summe kommt und somit dann zu einer schlechteren Approximation.
. Da dies zu Veränderungen in der b-Spalte führt, ist darauf zu achten, dass die Einträge in der b-Spalte nicht negativ werden oder dass es zu einer Vergrößerung der Summe kommt und somit dann zu einer schlechteren Approximation.
Um die Bedingungen für den Eintrag ![]() weiter einzugrenzen, werden die Veränderungen in der b-Spalte betrachtet. Nachdem ein Min-Schritt durchgeführt wurde, ergibt sich die neue b-Spalte aus der alten in folgender Weise. Die neuen Einträge sind durch eine Tilde über dem Buchstaben kenntlich gemacht.
weiter einzugrenzen, werden die Veränderungen in der b-Spalte betrachtet. Nachdem ein Min-Schritt durchgeführt wurde, ergibt sich die neue b-Spalte aus der alten in folgender Weise. Die neuen Einträge sind durch eine Tilde über dem Buchstaben kenntlich gemacht.
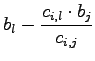 mit mit |
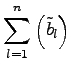 |
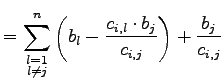 |
||
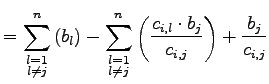 |
|||
 |
Der Wert des ersten Summanden ist größer Null, da mit einer gültigen Basislösung begonnen wurde und die b-Spalte somit nur positive Einträge hatte. Der dritte Summand ist ebenfalls positiv, da der Eintrag ![]() der vorherigen Basislösung ebenfalls positiv war, sowie der Eintrag
der vorherigen Basislösung ebenfalls positiv war, sowie der Eintrag ![]() . Daraus folgt, dass der zweite Summand einen Wert kleiner Null haben muss, um die Summe der Einträge zu verringern. Damit der Wert des zweiten Summanden kleiner Null ist, muss die Summe der Einträge in der i-ten Spalte ohne
. Daraus folgt, dass der zweite Summand einen Wert kleiner Null haben muss, um die Summe der Einträge zu verringern. Damit der Wert des zweiten Summanden kleiner Null ist, muss die Summe der Einträge in der i-ten Spalte ohne ![]() größer Null sein. Dies ergibt sich aus der Wahl des Eintrags
größer Null sein. Dies ergibt sich aus der Wahl des Eintrags ![]() , der bereits nach den oben genannten Voraussetzung positiv sein soll. Eine weitere Einschränkung für die Wahl von
, der bereits nach den oben genannten Voraussetzung positiv sein soll. Eine weitere Einschränkung für die Wahl von ![]() ist somit, dass die Summe der Einträge der Spalte, in der das
ist somit, dass die Summe der Einträge der Spalte, in der das ![]() gewählt wird, ohne
gewählt wird, ohne ![]() einen Wert größer Null haben muss, sowie der Eintrag
einen Wert größer Null haben muss, sowie der Eintrag ![]() einen ungleich Null, da ansonsten der zweite Summand den Wert Null hätte. Die Spalte in der das
einen ungleich Null, da ansonsten der zweite Summand den Wert Null hätte. Die Spalte in der das ![]() gewählt werden soll, kann sogar noch weiter eingeschränkt werden. Die folgenden Umformungen zeigen, dass die Summe ohne
gewählt werden soll, kann sogar noch weiter eingeschränkt werden. Die folgenden Umformungen zeigen, dass die Summe ohne ![]() sogar größer als Eins sein muss, um die Summe zu verringern.
sogar größer als Eins sein muss, um die Summe zu verringern.
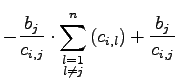 |
|||
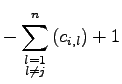 |
|||
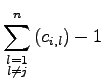 |
|||
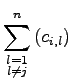 |
Ein Eintrag ![]() , der diese Voraussetzungen erfüllt, garantiert noch nicht, dass nach dem Min-Schritt mindestens ein Eintrag in der b-Spalte negativ ist. Somit muss, nachdem ein Eintrag nach diesen sehr einfachen Kriterien gefunden ist, geprüft werden, ob sich ein ungültiges Ergebnis ergibt.
, der diese Voraussetzungen erfüllt, garantiert noch nicht, dass nach dem Min-Schritt mindestens ein Eintrag in der b-Spalte negativ ist. Somit muss, nachdem ein Eintrag nach diesen sehr einfachen Kriterien gefunden ist, geprüft werden, ob sich ein ungültiges Ergebnis ergibt.
Damit die minimale Summe der b-Spalte und somit das bestmögliche Ergebnis gefunden wird, muss so oft ein Min-Schritt durchgeführt werden, bis kein dafür geeignetes Element mehr vorhanden ist. Durch Einsetzen der im Gleichungsystem stehenden Einträge in die genannten Formeln17, können die entsprechenden Kontrollpunkte berechnet werden.
Karl kleine Kruse 2007-09-16