Nächste Seite: Suchen der optimalen Bézierkurve Aufwärts: Konvexe Polygone Vorherige Seite: Aufstellen von Kriterien Inhalt
Aus den im vorherigen Kapitel genannten Bedingungen können Gleichungen aufgestellt werden, die den allgemeinen Verlauf der Bézierkurven im Verhältnis zu den Polygonecken beschreiben. Die in den Gleichungen verwendeten Variablen sollen hier definiert werden. Die Bedingungen für die elementaren Bézierkurven sollen an einem konkreten Polygonzug verdeutlicht werden. Dieser Polygonzug8 besteht aus vier Punkten, wobei Gleichungen für die mittlere Kante aufgestellt werden sollen. Der Polygonzug ist konvex und kann für einen beliebigen Teil eines konvexen Polygons stehen. Die Eckpunkte des Polygonzuges sind von ![]() bis
bis ![]() nummeriert. Da sich die Endpunkte der Bézierkurve durch die Verschiebung der Eckpunkte ergeben sollen, sind sie nach diesen benannt worden. Die Endpunkte der Bézierkurve lauten
nummeriert. Da sich die Endpunkte der Bézierkurve durch die Verschiebung der Eckpunkte ergeben sollen, sind sie nach diesen benannt worden. Die Endpunkte der Bézierkurve lauten ![]() und
und ![]() , wobei das ,,t`` im Namen verdeutlichen soll, dass der Punkt aus einem Eckpunkt hervorgeht, der um einen Parameter
, wobei das ,,t`` im Namen verdeutlichen soll, dass der Punkt aus einem Eckpunkt hervorgeht, der um einen Parameter ![]() verschoben ist.
verschoben ist.
Der Vektor, der vom Eckpunkt ![]() in Richtung Kontrollpunkt
in Richtung Kontrollpunkt ![]() der Bézierkurve zeigt, sei durch
der Bézierkurve zeigt, sei durch ![]() gegeben. Der entsprechende Vektor für
gegeben. Der entsprechende Vektor für ![]() sei mit
sei mit ![]() benannt. Der Vektor, der die Tangente an der Bézierkurve im Punkt
benannt. Der Vektor, der die Tangente an der Bézierkurve im Punkt ![]() angibt, sei mit
angibt, sei mit ![]() benannt sowie der im Punkt
benannt sowie der im Punkt ![]() mit
mit ![]() . Um alle Vektoren zu Vereinheitlichen, wird festgelegt, dass die Vektoren für die Verschiebung immer nach innen zeigen und die Richtungsvektoren der Tangenten immer in Richtung der Nummerierung, also in dem Teilstück von
. Um alle Vektoren zu Vereinheitlichen, wird festgelegt, dass die Vektoren für die Verschiebung immer nach innen zeigen und die Richtungsvektoren der Tangenten immer in Richtung der Nummerierung, also in dem Teilstück von ![]() zu
zu ![]() und von
und von ![]() zu
zu ![]() 9
9
![]() und
und ![]() sind definiert als die Summe des Vektors zu
sind definiert als die Summe des Vektors zu ![]() bzw
bzw ![]() und dem entsprechenden Richtungsvektor der Winkelhalbierenden, der mit einem entsprechenden Parameter
und dem entsprechenden Richtungsvektor der Winkelhalbierenden, der mit einem entsprechenden Parameter ![]() oder
oder ![]() multipliziert wird. Da die Punkte somit von den Parametern abhängig sind, können sie als Funktion angesehen. Also:
multipliziert wird. Da die Punkte somit von den Parametern abhängig sind, können sie als Funktion angesehen. Also:
Die Nummerierungen der Bezeichnungen der Parameter, soll die Zugehörigkeit zu einem Punkt verdeutlichen. So gehört zum Beispiel der Parameter ![]() zum Punkt
zum Punkt ![]() .
.
Da eine Verschiebung ins Innere des Polygonzuges definiert und eine Verschiebung nach Außen ausgeschlossen werden soll, weil dies einer schlechteren Approximation entsprechen würde, ergibt sich, dass die ![]() keinen negativen Wert annehmen dürfen.
keinen negativen Wert annehmen dürfen.
Die Vektoren ![]() sollen auf die Länge
sollen auf die Länge ![]() normiert sein, denn dann werden die Abstände zwischen den Endpunkten der elementaren Bézierkurve und denen der Polygonkante, durch die Parameter
normiert sein, denn dann werden die Abstände zwischen den Endpunkten der elementaren Bézierkurve und denen der Polygonkante, durch die Parameter ![]() und
und ![]() wiedergegeben. Der kürzeste Abstand zwischen der Bézierkurve und dem Polygon wird aber nicht immer durch die Werte der Parameter
wiedergegeben. Der kürzeste Abstand zwischen der Bézierkurve und dem Polygon wird aber nicht immer durch die Werte der Parameter ![]() und
und ![]() wiedergegeben, sondern sie repräsentieren den Abstand zwischen zwei bestimmten Punkten. Die Parameter können negative Werte abnehmen, was aber nicht erwünscht ist. Der Ausschluss dieser negativen Werte führt so zu einer besseren Approximation und schließt eventuell auftretende Sonderfälle aus.
wiedergegeben, sondern sie repräsentieren den Abstand zwischen zwei bestimmten Punkten. Die Parameter können negative Werte abnehmen, was aber nicht erwünscht ist. Der Ausschluss dieser negativen Werte führt so zu einer besseren Approximation und schließt eventuell auftretende Sonderfälle aus.
Die Parameter ![]() und
und ![]() werden als Indikatoren für die Abweichung der Bézierkurve vom Polygon festgesetzt, da sie die tatsächliche Verschiebung des Eckpunktes und somit einen Wert für die Veränderung des Polygons wiedergeben. Die kürzeste Strecke zwischen Eckpunkt und Bézierkurve ließe sich nicht durch eine lineare Gleichung beschreiben und würde ein komplett anderes Verfahren, welches auf quadratischen Gleichungen beruht, erfordern. Es ist zudem auch nicht notwendig die kürzeste Stecke zu verwenden, da der Wert der Verschiebung einen gleichwertigen Indikator darstellt, da durch ihn ein Verfahren ermöglicht wird, das auf linearen Gleichungen basiert und somit bei weitem nicht so komplex ist wie ein Verfahren das quadratischen Gleichungen beinhaltet.
werden als Indikatoren für die Abweichung der Bézierkurve vom Polygon festgesetzt, da sie die tatsächliche Verschiebung des Eckpunktes und somit einen Wert für die Veränderung des Polygons wiedergeben. Die kürzeste Strecke zwischen Eckpunkt und Bézierkurve ließe sich nicht durch eine lineare Gleichung beschreiben und würde ein komplett anderes Verfahren, welches auf quadratischen Gleichungen beruht, erfordern. Es ist zudem auch nicht notwendig die kürzeste Stecke zu verwenden, da der Wert der Verschiebung einen gleichwertigen Indikator darstellt, da durch ihn ein Verfahren ermöglicht wird, das auf linearen Gleichungen basiert und somit bei weitem nicht so komplex ist wie ein Verfahren das quadratischen Gleichungen beinhaltet.
Damit die elementaren Bézierkurven stetig ineinander übergehen, muss der 2. Kontrollpunkt, im Folgenden ![]() genannt, als Schnittpunkt der Tangenten der Endpunkte festgelegt werden. Dafür sind zwei weitere Parameter
genannt, als Schnittpunkt der Tangenten der Endpunkte festgelegt werden. Dafür sind zwei weitere Parameter ![]() und
und ![]() erforderlich.
erforderlich. ![]() ist durch die Parameter folgendermaßen festgelegt:
ist durch die Parameter folgendermaßen festgelegt:
Die elementare Bézierkurve wird nach dem Algorithmus von de Casteljau wie folgt festgelegt:
| (6) | |||
| (7) | |||
| (8) |
Es ist an dieser Stelle zu betonen, dass durch die Gleichungen keine Veränderung der Polygonzugkante beschrieben wird, die zu einer Bézierkurve führt, die das Polygon bestmöglich approximieren würde. Sondern es werden aufgrund der Lage der Eckpunkte des Polygons Gleichungen aufgestellt, welche die Lage der Kontrollpunkte der Bézierkurve beschreiben. Durch die Gleichungen sind alle Kontrollpunkte einer Bézierkurve nur noch in einem bestimmten Rahmen variabel. Der Graph der Bézierkurve kann nur in bestimmten Bereichen, welche durch die Gleichungen vorgegeben sind, verändert werden.
Die in den Gleichungen vorkommenden Parameter sollen, wie die Parameter ![]() und
und ![]() , auf positive Werte eingeschränkt werden. Die Einschränkung, dass
, auf positive Werte eingeschränkt werden. Die Einschränkung, dass ![]() nur positive Werte annehmen darf, führt dazu, dass die Bézierkurve nicht beliebig weit ins Innere des Polygonzuges geschoben werden kann. Negative Werte von
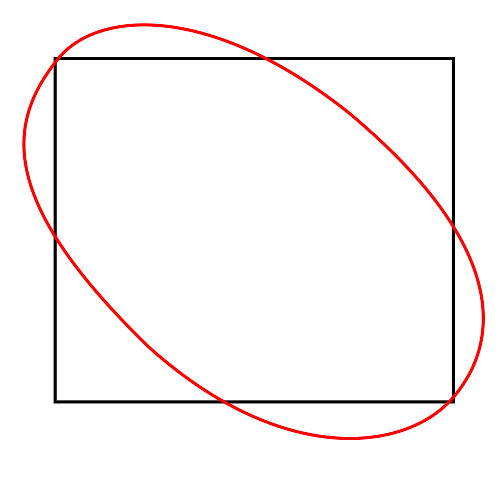
nur positive Werte annehmen darf, führt dazu, dass die Bézierkurve nicht beliebig weit ins Innere des Polygonzuges geschoben werden kann. Negative Werte von ![]() könnten zum Beispiel bei einem konvexen Polygon zu einem vollständigen Verlauf einer Bézierkurve innerhalb eines Polygons führen (siehe Abbildung 14). Dies wurde keiner Approximation eines Polygons, nach den genannten Kriterien entsprechen. In dieser Arbeit wird die Qualität der Approximation eines Polygons durch eine Bézierkurve, anhand der Summe der freien Parameter
könnten zum Beispiel bei einem konvexen Polygon zu einem vollständigen Verlauf einer Bézierkurve innerhalb eines Polygons führen (siehe Abbildung 14). Dies wurde keiner Approximation eines Polygons, nach den genannten Kriterien entsprechen. In dieser Arbeit wird die Qualität der Approximation eines Polygons durch eine Bézierkurve, anhand der Summe der freien Parameter ![]() und
und ![]() gemessen. Dabei gilt, dass die bestmöglichste Bézierkurve die geringste Summe der Parameter in den Gleichungen aufweist. Zudem führt ein negativer Parameter zu einer ungültigen Approximation.
gemessen. Dabei gilt, dass die bestmöglichste Bézierkurve die geringste Summe der Parameter in den Gleichungen aufweist. Zudem führt ein negativer Parameter zu einer ungültigen Approximation.
Für jede Kante von
![]() werden Gleichungen aufgestellt, die elementare Bézierkurven beschreiben, die diese Kante approximieren. Diese werden dann zu einem linearen Gleichungssystem zusammengefasst, das quadratische Bézierkurven beschreibt, die das gesamte Polygon approximieren. Diese Gleichungen sollen als Parameter nur noch
werden Gleichungen aufgestellt, die elementare Bézierkurven beschreiben, die diese Kante approximieren. Diese werden dann zu einem linearen Gleichungssystem zusammengefasst, das quadratische Bézierkurven beschreibt, die das gesamte Polygon approximieren. Diese Gleichungen sollen als Parameter nur noch ![]() und
und ![]() enthalten, die zur Bewertung der Approximation herangezogen werden. Diese Gleichungen werden nachfolgend vorgestellt. Die Bennennung erfolgt wiederum anhand des Polygonzuges aus Abbildung 12.
enthalten, die zur Bewertung der Approximation herangezogen werden. Diese Gleichungen werden nachfolgend vorgestellt. Die Bennennung erfolgt wiederum anhand des Polygonzuges aus Abbildung 12.
Zur Berechnung und Lösung von Gleichungen und Gleichungssystemen wurde das Computer Algebra System (CAS) Derive verwendet. Ein Ausdruck der jeweiligen Eingaben ist der beigelegten CD-ROM im PDF-Format beigefügt.
Nach Eingabe der Gleichungen 2 bis 9 in das CAS Derive, kann aus den Gleichungen 5 und 9 ein lineares Gleichungssystem aufgestellt werden, und dieses nach ![]() ,
, ![]() ,
, ![]() und
und ![]() gelöst werden. Das CAS Derive liefert als Ergebnis vier Gleichungen10. In den Gleichungen werden
gelöst werden. Das CAS Derive liefert als Ergebnis vier Gleichungen10. In den Gleichungen werden ![]() ,
, ![]() ,
, ![]() und
und ![]() jeweils in Abhängigkeit von
jeweils in Abhängigkeit von ![]() ,
, ![]() und
und ![]() beschrieben. Der Parameter
beschrieben. Der Parameter ![]() ist zwar frei wählbar, ist hier aber keine freie Variable. Der Wert von
ist zwar frei wählbar, ist hier aber keine freie Variable. Der Wert von ![]() soll zu Beginn der Approximation eines Polygons gewählt werden und geht somit nicht als freier Parameter in die Gleichungen ein, sondern als Konstante. Die Auswirkungen der Wahl des Wertes des Parameters werden in Kapitel 5.1 erläutert, da dies anhand der dann erstellten Bézierkurven einfacher ist.
soll zu Beginn der Approximation eines Polygons gewählt werden und geht somit nicht als freier Parameter in die Gleichungen ein, sondern als Konstante. Die Auswirkungen der Wahl des Wertes des Parameters werden in Kapitel 5.1 erläutert, da dies anhand der dann erstellten Bézierkurven einfacher ist.
Die vierte Gleichung (siehe Kapitel A.1.4) spielt in den folgenden Überlegungen eine zentrale Rolle. In dieser Gleichung wird das Verhältnis zwischen der Verschiebung der Eckpunkte ![]() und
und ![]() ins Innere des Polygonzuges und dem Abstand der Bézierkurve B zur Polygonkante beschrieben. Es soll mit Hilfe einer geringen Verschiebung
ins Innere des Polygonzuges und dem Abstand der Bézierkurve B zur Polygonkante beschrieben. Es soll mit Hilfe einer geringen Verschiebung ![]() und
und ![]() ein geringer Abstand
ein geringer Abstand ![]() erreicht werden. Diese Gleichung wird für jede Polygonkante eines konvexen Polygons mit
erreicht werden. Diese Gleichung wird für jede Polygonkante eines konvexen Polygons mit ![]() Kanten aufgestellt. Daraus ergeben sich
Kanten aufgestellt. Daraus ergeben sich ![]() Gleichungen, die alle Kriterien für eine quadratische Bézierkurve enthalten, und ein Gleichungssystem bilden. Eine solche Gleichung für eine Kante hat die allgemeine Form
Gleichungen, die alle Kriterien für eine quadratische Bézierkurve enthalten, und ein Gleichungssystem bilden. Eine solche Gleichung für eine Kante hat die allgemeine Form
| (10) |

|
Karl kleine Kruse 2007-09-16