Aufstellen von Kriterien

Für die folgenden Überlegungen, wie eine Bézierkurve verlaufen sollte, die ein konvexes Polygon approximiert, sei in Abbildung 6 ein Beispiel für ein solches Polygon gegeben, das im Folgenden mit $\overline {P}$ benannt wird.

Abbildung 6: Polygon $\overline {P}$ mit 6 Punkten, $\overline {P}$ mit einer Bézierkurve B, sowie nur die Bézierkurve B.

$\overline {P}$ besitzt eine endliche Anzahl von Punkten, hier sechs, welche das Polygon eindeutig festlegen. Die Punkte sind im Uhrzeigersinn von $P0$ bis $P5$ nummeriert. Polygone werden im Folgenden immer im Uhrzeigersinn nummeriert, so dass der Graph des Polygons immer eine Rechtskurve beschreibt.

Eine Kurve die $\overline {P}$ approximiert, sei durch eine quadratische Bézierkurve B gegeben. B besitze eine endliche Anzahl von Kontrollpunkten, durch die es eindeutig definiert ist.

Da B das Polygon $\overline {P}$ approximieren soll, sollte B eine Fläche begrenzen dessen Flächeninhalt mit dem der Fläche übereinstimmt, die von $\overline {P}$ begrenzt wird. Die Qualität der Approximation kann davon abhängig gemacht werden, wieviel von der Fläche, die das Polygon einschließt von der Bézierkurve eingeschlossen wird und ob beide eingeschlossenen Flächen den gleichen Flächeninhalt haben. Wenn eine Bézierkurve exakt die selbe Fläche einschließt, hat sie automatisch den gleichen Flächeninhalt und der Graph der Bézierkurve wäre identisch mit dem Graphen des Polygons, aber somit auch nicht mehr stetig. Eine Vergrößerung der Differenz der Flächen und der Flächeninhalte führt dann zu einer schlechteren Approximation. Der Flächeninhalt und die Fläche können somit als Kriterien angesehen werden. Dabei ist allerdings zu beachten, dass die Berücksichtigung dieser Kriterien nicht zu einer Übereinstimmung der Bézierkurve mit dem Polygon führen darf.

Eine weiteres Kriterium für den Grad der Abweichung zwischen Bézierkurve und Polygon ist die Summe der Abstandsquadrate. Wenn die Summe der Abstandsquadrate den Wert Null hätte, für beliebige Orte der Abstandsmessung, wäre der Graph der Bézierkurve ebenfalls mit dem des Polygons oder Polygonzuges identisch. Da dies wiederum nicht erstrebenswert ist, muss mit diesem Kriterium wie mit den obigen Kriterien verfahren werden.

Da der wesentliche Unterschied zwischen $\overline {P}$ und B darin besteht, dass B keine Ecken besitzt, muss eine Umwandlung von $\overline {P}$ zu B die Abrundung der Ecken von $\overline {P}$ beinhalten. Wenn B den gleichen Flächeninhalt wie $\overline {P}$ haben soll, kann das nur durch einen Flächenverlust an den Ecken geschehen, der zwischen den Ecken kompensiert wird. Eine Flächenzunahme an den Ecken müsste durch eine Flächenabnahme zwischen den Ecken kompensiert werden und würde die Summe der Abstände im Allgemeinen erhöhen. Dazu ist in Abbildung 7 ein Beispiel gegeben.

Abbildung 7: Polygon $\overline {P}$ mit einer Bézierkurve B.

Ein Polygon kann als Zusammensetzung von Kanten angesehen werden. $\overline {P}$ hat dann sechs Kanten, welche die Eckpunkte verbinden. Da ein Polygon beliebig viele Kanten aufweisen kann, ist es sinnvoll, wenn B so aus elementaren Bézierkurven zusammengesetzt ist, dass es für jede elementare Bézierkurve $C_{i}$ von B eine Kante $K_{i}$ von $\overline {P}$ gibt, die von $C_{i}$ approximiert wird. So können Bedingungen für jedes $C_{i}$ aufgestellt werden aus denen dann B hervorgeht.

Für jede Kante von $\overline {P}$ muss dann eine elementare quadratische Bézierkurve aufgestellt werden, so dass diese stetig ineinander übergehen, um eine nach den genannten Kriterien bestmögliche Bézierkurve zu erhalten.

Alternativ können Gruppen von Kanten durch eine elementare Bézierkurve approximiert werden. So würde die Komplexität der Bézierkurve verringert werden. Darauf soll in Kapitel 5.3 genauer eingegangen werden. Die einzige Einschränkung, die hier an das Polygon gestellt wird, ist dass keine drei benachbarten Punkte auf einer Geraden liegen und somit für den Graphen des Polygons der mittlere Punkt überflüssig ist.

Die Bézierkurve, die eine Kante eines Polygons approximieren soll, muss auch Kriterien erfüllen, die den Verlauf der Bézierkurve beschreiben. Diese Kriterien sollen nachfolgend vorgestellt werden.

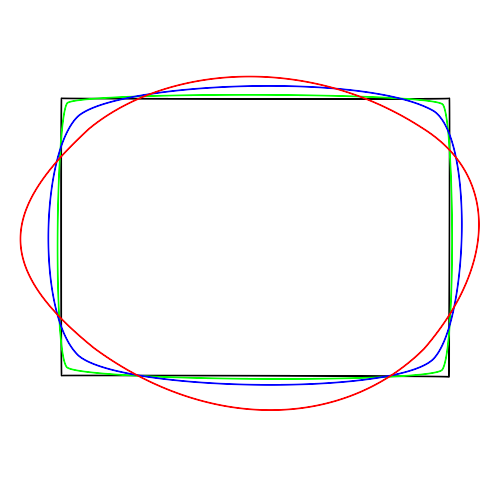
Eine quadratische elementare Bézierkurve ist durch drei Kontrollpunkte definiert: Einen Anfangs- und einen Endpunkt, sowie einen Kontrollpunkt, der die Krümmung angibt und der durch den Schnittpunkt der Tangenten an den Endpunkten festgelegt ist. Eine Umwandlung einer Kante in eine entsprechende Bézierkurve durch Flächenabnahme an den Ecken könnte durch eine Verschiebung der Eckpunkte des Polygons in das Polygon beschrieben werden. Die Endpunkte der Kante sind dann, vor der Verschiebung ins Innere, den Endpunkten der elementaren Bézierkurve gleich zu setzen. Die Punkte müssen auf einem vorher beschriebenen Weg, abhängig von den Nachbarkanten, im einfachsten Fall einer Geraden, verschoben werden. Die Flächenzunahme zwischen den Eckpunkten des Polygons entspricht einem Verschieben des mittleren Kontrollpunktes vom Polygon weg. Je weiter die Eckpunkte des Polygons ins Inneren verschoben werden, desto mehr müssen die mittleren Kontrollpunkte nach Außen wandern, um den Flächenverlust auszugleichen. Eine mögliche Entwicklung vom Polygon zur Bézierkurve ist in der Abbildung 8 gezeigt.

Abbildung 8: Eine möglich Entwicklung von einem Polygon zu einer Bézierkurve, welche das Polygon approximieren würde.

Die Verschiebung der Eckpunkte erfolgt auf einer Geraden, da sie die geringste Komplexität besitzt. Damit die Verschiebung für beliebige Winkel zwischen den Nachbarkanten ins Innere des Polygons führt, soll die Winkelhalbierende zwischen zwei Kanten als Richtungsvektor der Verschiebung des entsprechenden Eckpunktes gewählt werden. Die Winkelhalbierende lässt sich nicht ohne größeren Aufwand, wie zum Beispiel das Wurzelziehen in den reellen Zahlen, berechnen. Sie ist aber eine Gerade, die für jeden Winkel, den die Kanten einschließen ins Innere des Polygons führt und keine der Kanten bei der Verschiebung bevorzugt.

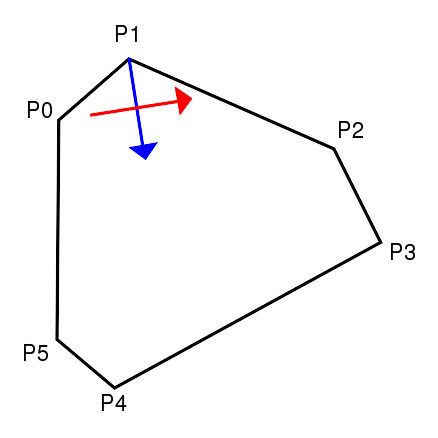
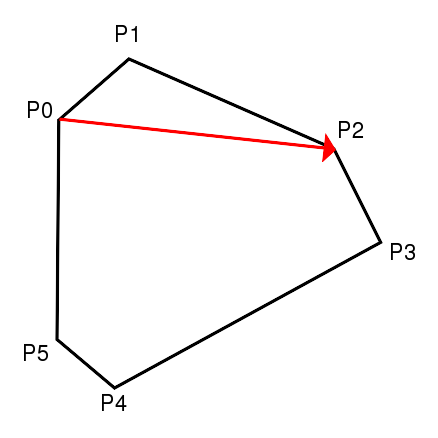
Es ist ein Tangentenvektor festzulegen, damit ein stetiger Übergang von einer Teilkurve $C_{i}$ zur nächsten Teilkurve erfolgt, der für Kurvenstücke die ineinander übergehen einen stetigen Übergang erzeugt. In den verschobenen Eckpunkten, die den Übergang von einer elementaren Bézierkurve zur nächsten beschreiben, muss für einen stetigen Übergang der Tangentenvektor für beide elementaren Bézierkurven in dem Endpunkt gleich sein. Der Tangentenvektor ist weiterhin abhängig von den Kanten am jeweiligen Eckpunkt des Polygons, da sich die Kurve in dem jeweiligen Punkt beiden bestmöglichst anpassen sollte. Es gibt verschiedenen Möglichkeiten die Tangente in den Endpunkten zu definieren. Eine Möglichkeit ist den zur Winkelhalbierenden senkrechten Vektor als Tangentenvektor zu wählen (siehe Abbildung 9). In diesem Fall ist der Winkel, der mit jeder der Kanten eingeschlossen wird, gleich groß. Eine bessere Approximation der Kanten ist aber mit einem anderen Vektor möglich. Wenn der Tangentenvektor von den, dem Eckpunkt an dem die Bézierkurven zusammentreffen, benachbarten Eckpunkten definiert wird (siehe Abbildung 10), ergibt sich eine geringere Abweichung. Dies soll im Folgenden erläutert werden.

Abbildung 9: Richtungsvektor der Winkelhalbierenden in $P1$ (blau) und einen Richtungsvektor (rot) der zur Winkelhalbierenden senkrecht steht.
Abbildung 10: Vektor von $P0$ zu $P2$ der als Richtungsvektor für die Tangente im Endpunkt der Bézierkurve bei $P1$ dienen soll

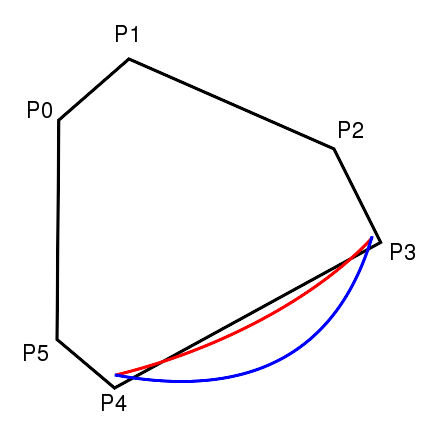
Ist eine Kante im Vergleich zu der Nachbarkante sehr viel länger, ist es von Vorteil, wenn der Tangentenvektor in den Ecken an den Bézierkurven diesem Umstand Rechnung trägt. Die Bézierkurve muss an einer langen Kante deutlich flacher verlaufen, um die Summe der Abstände niedrig zu halten. Ein zu steiler Winkel an den Eckpunkten würde zu einem großen Abstand zwischen Polygon und Bézierkurve führen. Wenn der Tangentenvektor nun durch die benachbarten Eckpunkte definiert wird (siehe Abbildung 11), führt eine lange Kante zu einer flachen Kurve, da der Tangentenvektor einen kleinen Winkel mit der entsprechenden Kante einschließt und der Kontrollpunkt somit nahe an der Kante liegt. Bei kurzen Kanten führt dies zu einem gegenteiligen Effekt, da an diesen Stellen ein steiler Winkel entsteht. An den kurzen Kanten ist der Zuwachs an Abweichung aber im Gegensatz zur Abnahme an Abweichung an den langen Kanten geringer. Also wird der durch die benachbarten Eckpunkte definierte Richtungsvektor als Tangentenvektor der Bézierkurve an den Endpunkten verwendet.

Abbildung 11: Je eine Bézierkurve mit dem Richtungsvektor der Senkrechten der Winkelhalbierenden als Tangentenvektoren (blau) und dem Richtungsvektor der durch die benachbarten Punkte gegeben ist.