Nächste Seite: Die Implementation Aufwärts: Die Auswirkungen der Parameter Vorherige Seite: Modifikator der kubischen Bézierkurven Inhalt
In Kapitel 3 wurde erläutert, dass zur Approximation eines Polygons oder Polygonzuges Kanten zu Gruppen zusammengefasst werden können, so dass für jede Gruppe eine elementare Bézierkurve verwendet wird. Auf diese Weise wird die Komplexität der gesamten Bézierkurve verringert. Die Gruppen müssen so gebildet werden, dass der Grad der Approximation sich durch das Bilden der Gruppen nicht wesentlich verschlechtert. Stattdessen sollte er sich sofern möglich sogar verbessert.
Die Zusammenfassung zu Gruppen kann vor der Approximation durch Zusammenfassen von geeigneten Nachbarkanten oder nach der Approximation durch vereinfachen der Bézierkurve, durch Ersetzen von benachbarten elementaren Bézierkurven durch eine elementare Bézierkurve, erfolgen. Das Zusammenfassen nach der Approximation hat den Vorteil, dass der Graph der Bézierkurve festgelegt ist und somit eine Vergrößerung der Abweichung nach der Zusammenfassung von Teilen der berechneten Bézierkurve gut festgestellt werden kann. Die Wahl der zusammengefassten Kanten kann dann, entsprechend dieser Erkenntnisse verändert werden. Der Nachteil ist allerdings, dass das Optimierungsverfahren auf alle elementaren Bézierkurven angewendet wird. Dies kann bei einem konvexen Teilsegment mit vielen Kanten sehr aufwendig werden, wobei es anschließend zu einem Zusammenfassen von vielen elementaren Bézierkurven kommen kann. Dieser Aufwand kann durch das Zusammenfassen der Kanten vor der Approximation verhindert werden. Der Nachteil dieser Möglichkeit ist, dass sich das Zusammenfassen kaum auf den Verlauf der Bézierkurve beziehen lässt, da diese erst nach dem Optimieren feststeht. Somit können mögliche Auswirkungen auf die neue Bézierkurve durch das Bilden von Gruppen vorab nicht berücksichtigt werden.
Hier werden die Kanten vor der Approximation zu Gruppen zusammengefasst, um die Laufzeit der Approximation gering zu halten. Die Laufzeit und der Bedarf an Speicherplatz für die Berechnungen wachsen, bezogen auf die Anzahl der Kanten aufgrund des Gleichungssystems mindestens exponentiell, was im Fall von vielen kurzen Kanten zu einer nicht zu bewältigenden Datenmenge führen kann. Daher hat das Verringern der Abweichung durch das Zusammenfassen von Kanten, im Gegensatz zu der Verringerung des benötigten Speicherplatzes, eine untergeordnete Bedeutung.
Für die Art und Weise der Zusammenfassung von Kanten gibt es ebenfalls zwei Möglichkeiten. Bei der ersten Möglichkeit werden die Kanten so zu Gruppen zusammengefasst, dass für jede Gruppe eine elementare Bézierkurve aufgestellt werden kann, wobei jede Kante als Bedingung in die elementare Bézierkurve der Gruppe eingeht. Dieses Verfahren kann allerdings ebenfalls zu einer übermäßig großen Datenmenge führen. Bei der zweiten Möglichkeit werden die Kanten so zu Gruppen zusammengefasst, dass für die Approximation nur die äußeren beiden Punkte der Gruppe verwendet werden. Die Gruppe von Kanten muss dann so gewählt werden, dass die mittleren Punkte für die Approximation vernachlässigt werden können. Da die Verringerung des Speicherplatzes im Vordergrund steht, wird hier die zweite Möglichkeit verwendet.
Das zu approximierende Polygon kann mit dem gewählten Verfahren auf folgende Weise nach und nach vereinfacht werden. Für jeden Eckpunkt des Polygons wird geprüft, ob er für die Approximation nötig ist, falls dies nicht der Fall ist, wird er vernachlässigt. Andernfalls wird zum nächsten Punkt übergegangen. Dieses Vernachlässigen entspricht der Bildung einer Gruppe aus den Kanten, zu denen der Eckpunkt gehört. Nachdem dieses Verfahren abgeschlossen ist, bleibt ein Polygon übrig, dass keine Punkte enthält, die nach vorgegebenen Kriterien überflüssig sind.Diese Kriterien sollen im Folgenden erläutert werden.
Ein Eckpunkt ist für die Approximation unnötig, wenn eine der zugehörigen Kanten zu kurz ist. Dies ist relativ zur gesamten Bildgröße, sowie zur gewünschten Auflösung des Bildes zu dem die berechnete Bézierkurve gehört, zu sehen. Angenommen die zu approximierenden Polygone sind auf einer Abbildung dargestellt mit 500 mal 500 Bildpunkten. Darüber hinaus sollen die Polygone Kanten besitzen, die nur 5 Bildpunkte lang sind. Eine Bézierkurve, die für diese Polygone berechnet wurde, die in der gleichen Auflösung dargestellt werden soll, ist an dieser Kante kaum von der Kante zu unterscheiden. Wenn die Kanten an den entsprechenden Punkt einen Winkel von ca. 180^&cir#circ; einschließt, ändert sich der Graph des Polygons kaum, wenn der Punkt nicht berücksichtigt wird. Die an den Punkt gestellten Kriterien sind somit die Länge der zugehörigen Kanten, der Winkel im Eckpunkt und die verwendete Auflösung bei der Darstellung.
Der Wert, der herangezogenen wird, um zu prüfen, ob ein Polygon oder Polygonzug konvex ist, gibt auch Aufschluss darüber, ob diese Kriterien in einem Eckpunkt erfüllt werden. Dieser Wert (siehe 2.5ff) entspricht dem Flächeninhalt der Fläche, der von den Vektoren aufgespannt wird. Wenn dieser Flächeninhalt sehr gering ist, schließen die Vektoren einen kleinen Winkel ein oder bzw. und haben eine geringe Länge. Aus einem komplexen Polygon, das viele kurze Kanten besitzt kann durch das Vernachlässigen derjenigen Eckpunkte, deren Kanten einen Grenzwert unterschreiten, ein einfacheres Polygon berechnet werden, dessen Bézierkurve keine große Abweichung vom Originalpolygon aufweist.
Auf Seite 36 sind drei verschiedene Beispiele für die Wahl des Parameters gezeigt.

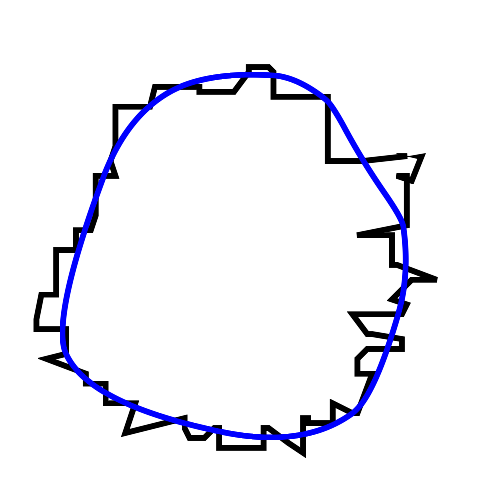
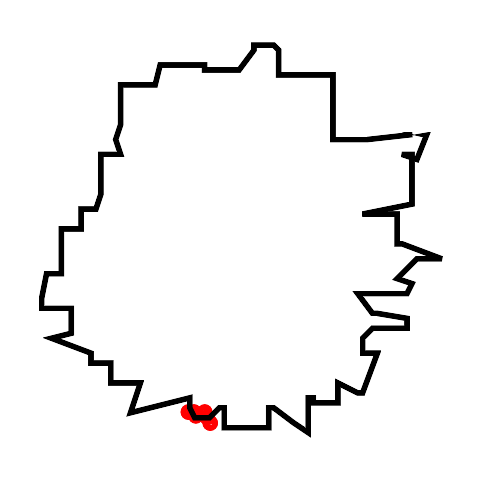
|
Karl kleine Kruse 2007-09-16