Nächste Seite: Approximation durch quadratische Bézierkurven Aufwärts: Grundlagen Vorherige Seite: Algorithmus von de Casteljau Inhalt
Eine Art den Begriff ,,Konvex`` zu definieren ist folgender Definition zu entnehmen:
Ein Polygon oder Polygonzug ist konvex, wenn die Strecke zwischen zwei beliebigen Punkten, die innerhalb der vom Polygon oder Polygonzug begrenzten Fläche liegen, immer komplett innerhalb der vom Polygon oder Polygonzug begrenzten Fläche liegt.
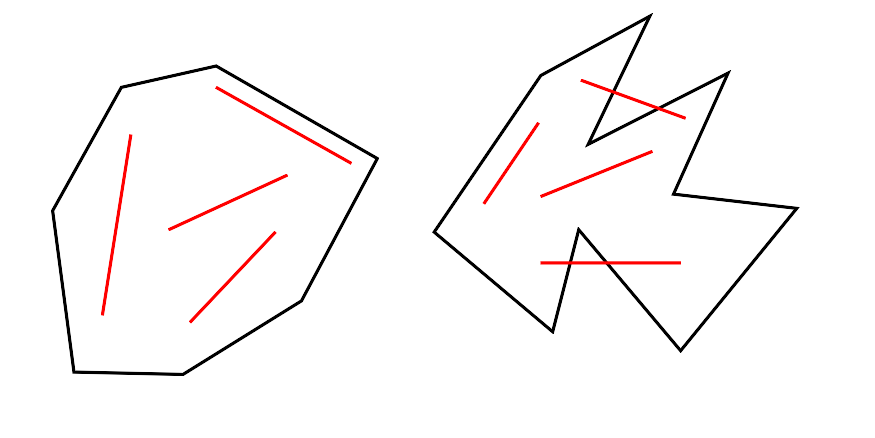
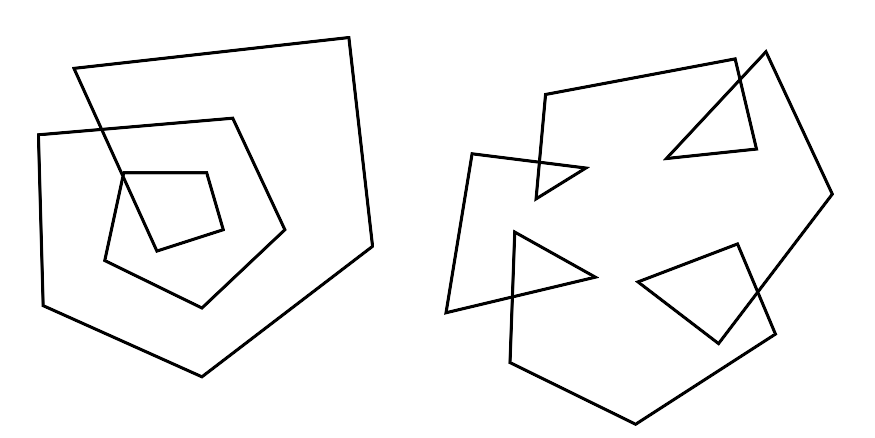
In Abbildung 1 ist sowohl ein Beispiel für ein konvexes als auch für ein nicht konvexes Polygon gegeben. In Abbildung 2 sind Polygone gezeigt, die nach der gegebenen Definition als nicht Konvex angesehen werden. Da diese Polygone in dieser Arbeit ebenfalls als konvex angesehen werden sollen, da die vorgestellte Approximation diese nach dem gleichen Verfahren behandelt, benötigten diese eine andere Definition des Begriffes ,,Konvex``. Deswegen ist die in den folgenden Kapiteln angewendete Definition folgende.
Ein Polygon oder Polygonzug ist konvex, wenn der Graph des Polygons bzw. Polygonzuges durchgehend eine Linkskurve oder eine Rechtskurve beschreibt.
Mathematisch kann das durch folgende Formeln ausgedrückt werden:
Ein Polygon ist konvex, wenn eine von den folgenden Aussagen für allemit
zutrifft:
oder
Ein Polygonzug ist konvex, wenn eine von den folgenden Aussagen für allemit
zutrifft:
oder
|
Der Operator ![]() hat dabei folgende Definition:
hat dabei folgende Definition:
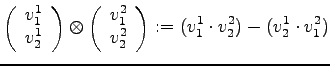 |
Dieser Operator ergibt sich aus den nachfolgenden Überlegungen:
Jedem Vektor aus der Euklidischen Ebene kann ein Vektor im
![]() zugeordnet werden, der durch ergänzen des Vektors um einen Eintrag mit dem Wert Null entsteht. Also
zugeordnet werden, der durch ergänzen des Vektors um einen Eintrag mit dem Wert Null entsteht. Also
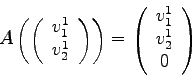 |
Die Euklidische Ebene ist dann im
![]() eingebettet. Das Spatprodukt dreier Vektoren
eingebettet. Das Spatprodukt dreier Vektoren ![]() ,
, ![]() und
und ![]() aus dem
aus dem
![]() ist definiert als
ist definiert als
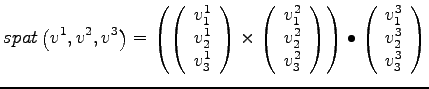 |
Das Vorzeichen dieses Spatproduktes gibt an ob es sich bei dem System von Vektoren um ein Links- oder Rechtssystem handelt. Dadurch kann mit Hilfe dieser eingebetteten Euklidischen Ebene folgende Funktion aufgestellt werden.
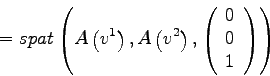 |
|||
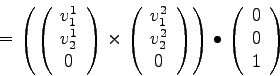 |
|||
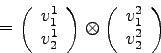 |
In der Funktion ![]() wurde das Spatprodukt der eingebetteten Vektoren und dem auf der eingebetteten Euklidischen Ebene senkrechten Einheitsvektor gebildet. Wenn die Reihenfolge der eingebetteten Vektoren in der Funktion vertauscht werden, ist das äquivalent zu einem Richtungswechsel. Das System der Vektoren wechselt dann ebenfalls die Richtung, wie das Vorzeichen des Spatproduktes. Somit kann die genannte Formel für die Bestimmung der Richtungswechsel genutzt werden.
wurde das Spatprodukt der eingebetteten Vektoren und dem auf der eingebetteten Euklidischen Ebene senkrechten Einheitsvektor gebildet. Wenn die Reihenfolge der eingebetteten Vektoren in der Funktion vertauscht werden, ist das äquivalent zu einem Richtungswechsel. Das System der Vektoren wechselt dann ebenfalls die Richtung, wie das Vorzeichen des Spatproduktes. Somit kann die genannte Formel für die Bestimmung der Richtungswechsel genutzt werden.
Folgende Abbildungen sollen das Verfahren zum Erkennen eines Richtungswechsels verdeutlichen.
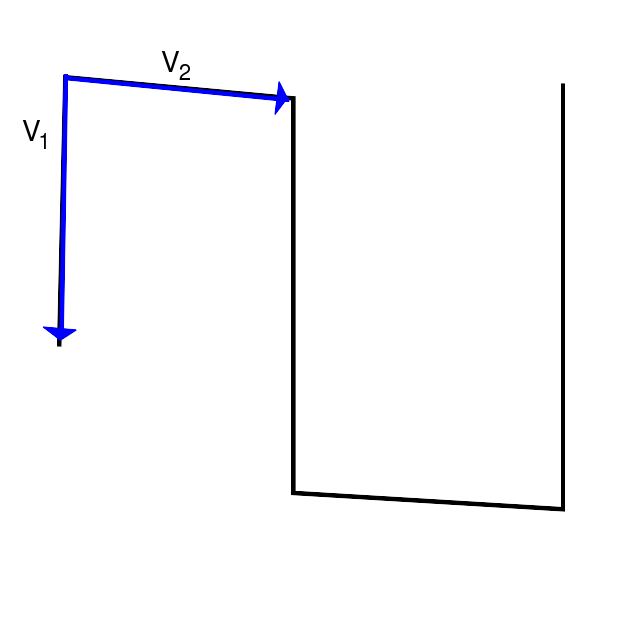
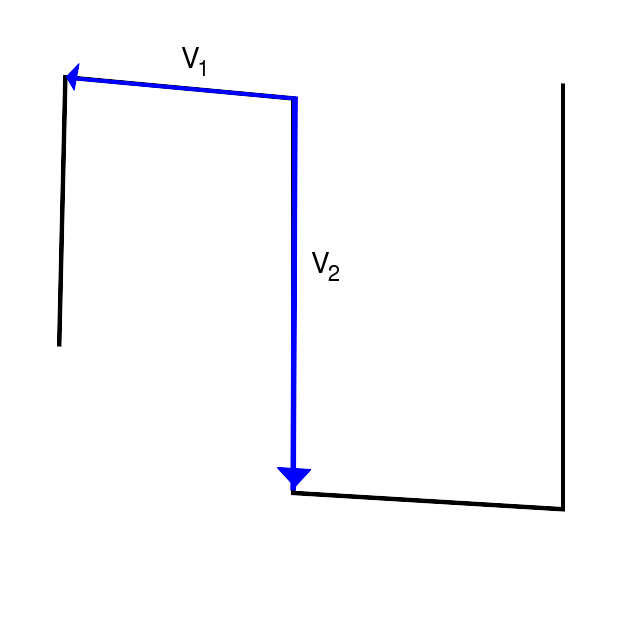
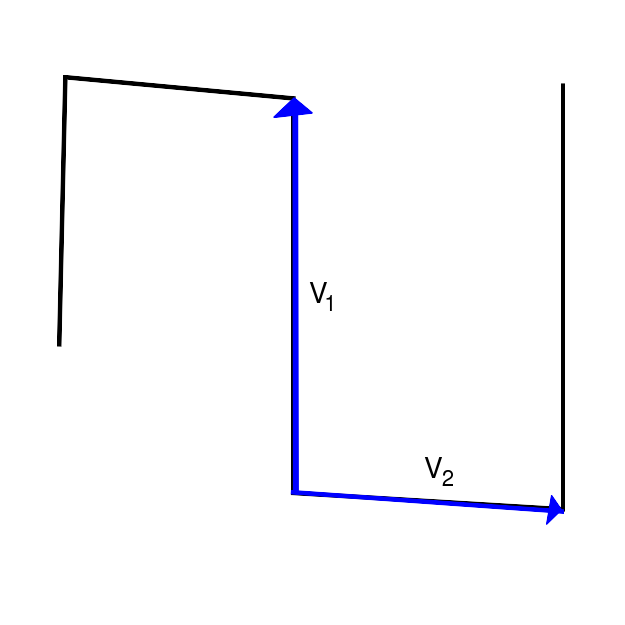
|
Karl kleine Kruse 2007-09-16