Nächste Seite: Algorithmus von de Casteljau Aufwärts: Grundlagen Vorherige Seite: Polygonzug Inhalt
Bézierkurven sind Graphen spezieller Polynomfunktionen. Sie werden vielfach verwendet, um stetige Kurven in vektorgraphischen Formaten zu speichern. Eine Bézierkurve ist eine Funktion
![]() . Bézierkurven können in allen Potenzen des Zahlenraumes
. Bézierkurven können in allen Potenzen des Zahlenraumes
![]() auftreten, wobei in Bézierkurven der Potenz
auftreten, wobei in Bézierkurven der Potenz ![]() die Bernsteinpolynome vom Grad
die Bernsteinpolynome vom Grad ![]() der folgenden Form vorkommen.
der folgenden Form vorkommen.
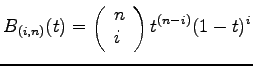 mit mit |
Da die Speicherung in zweidimensionaler Form erfolgt, wird im weiteren Verlauf der Raum in den die Bézierkurve abbildet auf die Euklidische Ebene eingeschränkt. Des Weiteren werden Bézierkurven, deren Funktion als höchste Potenz den Grad zwei hat, quadratische Bézierkurven genannt, sowie die der Potenz drei kubische Bézierkurven.
Der Verlauf einer Bézierkurve vom Grad ![]() in der Euklidischen Ebene ist festgelegt durch ein Tupel von
in der Euklidischen Ebene ist festgelegt durch ein Tupel von ![]() Punkten die Kontrollpunkte genannt werden. Die entsprechende Funktion der Bézierkurve hat folgende Form:
Punkten die Kontrollpunkte genannt werden. Die entsprechende Funktion der Bézierkurve hat folgende Form:
Die Graphen dieser Funktionen sollen im Folgenden als elementare Bézierkurven angesehen werden. In graphischen Applikationen wird der Name Bézierkurve meist für eine aus elementaren Bézierkurven zusammengesetzte Kurve verwendet, in der die elementaren Bézierkurven stetig ineinander übergehen. Diesem Unterschied soll durch die verschiedenen Bezeichnungen Rechnung getragen werden. Wenn im Folgenden Bézierkurven genannt werden, ist eine Sammlung von elementaren Bézierkurven gemeint, deren Graphen als Gesamtbild eine stetige Kurve in der Euklidischen Ebene erzeugen.
Innerhalb einer Bézierkurve lässt sich der stetige Übergang des Graphen einer elementaren Bézierkurve zum nächsten sich durch zwei Bedingungen erreichen. Zum einen müssen Endpunkt der einen elementaren Bézierkurve und Anfangspunkt der anderen identisch sein. Zum anderen müssen die Geraden, welche den Tangenten in den Endpunkten entsprechen, übereinstimmen, wobei die Tangenten in den Endpunkten durch die Kontrollpunkte festgelegt sind.
Für quadratische Bézierkurven sind die Tangenten durch den jeweiligen Endpunkt, also den jeweiligen Kontrollpunkt, und den mittleren Kontrollpunkt gegeben. Für kubische Bézierkurven sind die Tangenten durch die Endpunkte und den jeweils benachbarten Kontrollpunkt gegeben. Weitere Informationen zu Bézierkurven können unter anderem bei Wikipedia [4] entnommen werden.
Karl kleine Kruse 2007-09-16